Rayleigh's method for natural frequencies

 Rayleigh's method for natural frequencies

Rayleigh gave  the following strategy to determine the natural frequencies of dynamic systems.

1. The total response is resolved into spatial and time variations. This is always true for systems vibrating under natural modes
2. Any spatial variation that satisfies the boundary conditions can be assumed. Accordingly, the result will be only approximate.
3. The temporal (time-) distribution will be simple harmonic motion (under natural vibration)
4. Using the total response the expression for the strain energy can be derived
5. Using the total response, the expression for the kinetic energy can also be derived
6. Assuming no damping, the maximum values of strain energy and kinetic energies can be equated to give the expression for natural frequency.

These steps are demonstrated in the figures below

The solution for natural vibration of simply supported beam 

(* This solution assumes that the gravity is absent. Otherwise we will have to consider the change in potential energy during the vibration. Alternatively this can be assumed to be a vertical simply supported column) 

The solution for the above problem can also be derived from first principles as follows

The solution for natural vibration of cantilever beam 

(* This solution assumes that the gravity is absent. Otherwise we will have to consider the change in potential energy due to the vibration. Alternatively this can be assumed to be a vertical cantilever column)

Solution in one step using the derived expression for wn. 

Note that the assumed shape function should satisfy the boundary conditions at the ends

The above solution can also be derived from first principles as follows

Rayleigh method can also be applied to lumped mass system as follows

  From this the Rayleigh coefficient can be calculated as wn2=32/170

From this the Rayleigh coefficient can be calculated as wn2=275/200

Plastic ANalysis of Structures

 PLASTIC ANALYSIS OF STRUCTURES

The plastic behaviour is studied at three levels

1. Material level
2. section level
3. Member level
4. structure level

QUESTION BANK

Section Level Problems

            Find the shape factors for the sections shown below

Member level problems

               Determine the load factor for the following structures

         

Structure Level Problems

Membrane Theory for Shells of Revolution

 Membrane Theory for Shells of Revolution

Membrane analysis of cylindrical shells

Membrane Analysis of Cylindrical shells 

 

STIFFENESS MATRIX METHOD

 STIFFNESS MATRIX METHOD

LEVEL: Undergraduate (B. Tech )

In this method you have two major stages

1. Generation of stiffness matrix
2. Use of stiffness matrix to solve structural analysis problems

Generation of stiffness matrix

The stiffness matrix can be generated using either direct method OR transformation method

Transformation method

The transformation method has the following steps

1. Generation of member stiffness matrix [K_m
2. Generation of transformation matrix [C]
3. Obtaining system stiffness matrix using [C^T][K_m][C] 

 EXAMPLE: Truss Analysis using Stiffness matrix method

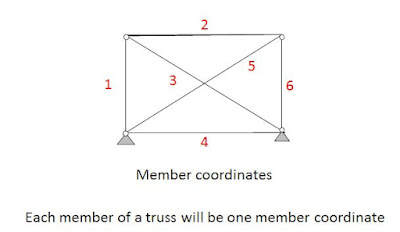
Step1: Mark system coordinates and member coordinates

Step2: Write member stiffness matrix. 

For truss each member has 1x 1 stiffness matrix [AE/L ]

Step3: Write transformation matrix. 

So, the size of transformation matrix will be  (no. of members x no. of DoF). For determining the elements of each column of C matrix, give unit displacement along SYSTEM coordinates and find displacements along member coordinates (Axial extensions)

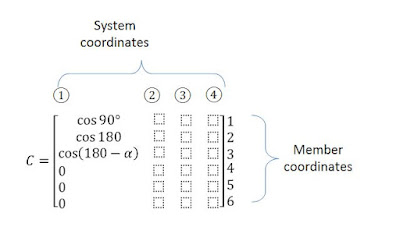
It can be observed that when unit displacement is given as shown above, the members 1,2,3 gets deformed. So, non-zero values will be there ONLY in rows 1,2,3 of Column 1. These non-zero values will be equal to cosθ , where θ is the anti-clock wise angle made by the rotating member from the positive x-axis direction. (see left portion of the figure below)

For member1, the value of θ is +90͒, for member2, the value of θ is 180͒, for member3, the value of θ is 180͒-θ. (see figure below)

So, the first column of C matrix will be 

For the second column of C, the deformed shape will be as shown below

In this case also, the value of θ for various members will remain same, because the unit displacement is occuring at the same joint. But, since the unit displacement is in y-direction, the extension of each member will be sinθ. So, the second column of C matrix will be 

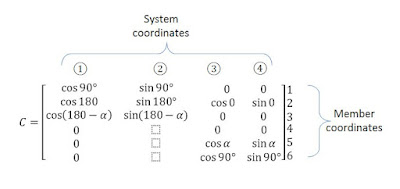
For the third column of C, the deformed shape will be as shown below

 

 In this case, the mebers 1,3,4 are not deformed, and so will have zero extensions. FOr mebers 2,5, 6 the angle θ will be 0͒, α, 90͒. Since the unit displacement is horizontal, the extension will be cosθ. Thus the third column of C will be

The deformed shape for the fourth column will be obtained by giving unit displacement along system coordinate 4 and zero displacement alon all other system coordinates

 

In this case also, the angle θ will remain same as in the previous case (because the unit displacement occurs at the same joint). But, the extension becomes sinθ, because the unit displacement is given in the vertical direction. Thus, the C matrix will be as follows

Final C matrix will be 

Summary of [C] matrix

 

The system stiffnes matrix will be [K]=[C^T][K_m][C]