Slope deflection method for beams

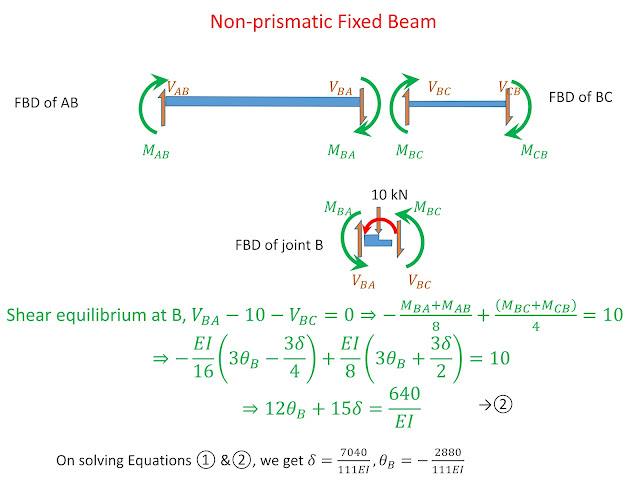
This blog post illustrates the use of the slope-deflection method to analyse indeterminate beams

 The following steps are followed in the slope-deflection method 

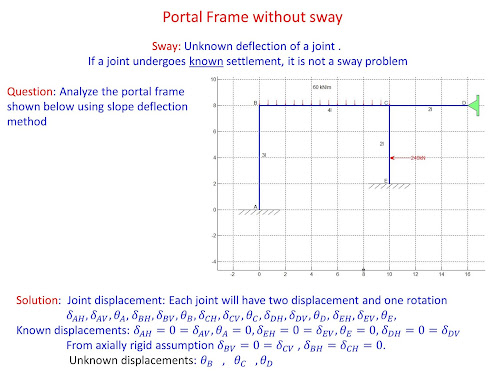
1.  Identifying the unknown joint displacements /kinematic indeterminacy/Degree of Freedom (DOFs)
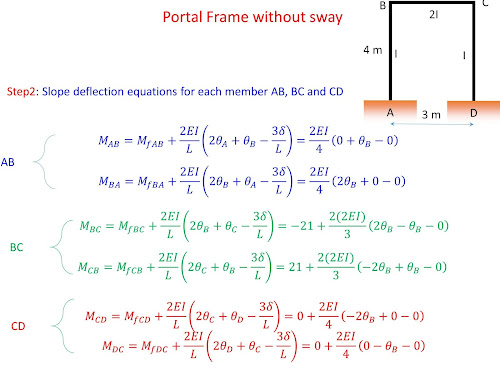
2.  Write slope deflection equations (SDEs) for each member. This includes substituting the fixed end moments (due to span loading) in SDEs, substituting known joint displacements in each SDE
3. Write the joint equilibrium equations for each joint having a DOF. Substituting SDEs in joint equilibrium equations
4. Solve the joint equilibrium equations simultaneously for unknown joint displacements
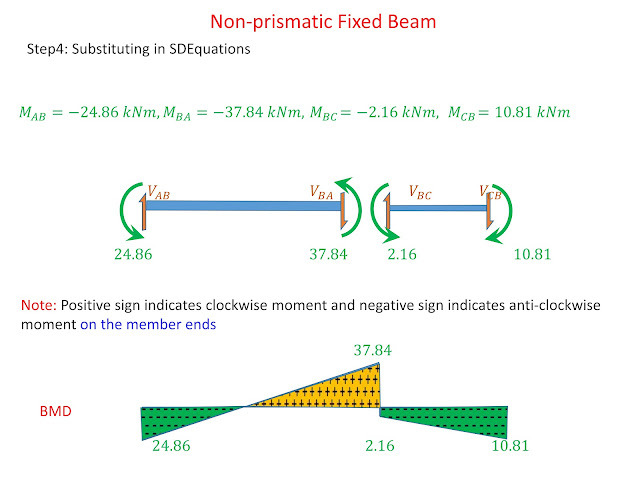
5. Substituting the joint displacements in SDEs to evaluate the member end moments
6. Drawing the deflected shape and BMD for the frame

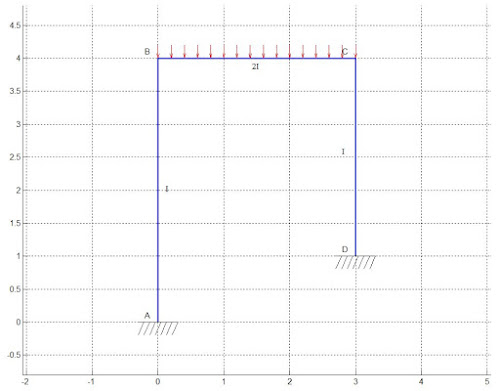
                 Illustrative Example-1                             

In the two-span continuous beam given below, there is only one kinematic indeterminacy (or unknow joint displacement). That is, the rotation at B (or slope at B)

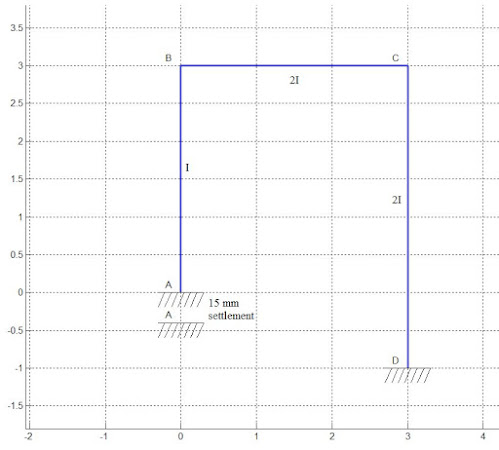
                             Illustrative Example-2                                          

In this example, there are two unknown joint displacements (Kinematic indeterminacy=2). These are the rotations at joints B and C

            Illustrative Example-3                                

Slope Deflection Method for portal Frames

 The following content explains the procedure for 

1.  identifying the unknown joint displacements /kinematic indeterminacy/Degree of Freedom (DOFs)
2.  writing slope deflection equations (SDEs) for each member 
3. substituting the fixed end moments (due to span loading) in SDEs
4. substituting known joint displacements in each SDE
5. writing the joint equilibrium equations for each joint having a DOF
6. Substituting SDEs in joint equilibrium equations
7. Solving the joint equilibrium equations simulateously for unknown joint displacements
8. Substituting the joint displacements in SDEs to evaluate the member end moments
9. Drawing the deflected shape and BMD for the frame

Problem 1

Problem 2

Analysis of portal frame "with sway" using Slope deflection method

Exercise Problems:

Ex.1

The UDL on the beam BC is 28 kN/m.

Answer for above problem is: M_AB=5.83 kN-m, M_BA=10.07 kN-m, M_BC=-10.07 kN-m, M_CB=8.9 kN-m, M_CD=-8.9 kN-m, M_DC=-3.04 kNm

       Ex.2

Answer for above problem is: M_AB=-35.08 kN-m, M_BA=-20.92 kN-m, M_BC=20.92 kN-m, M_CB=52.92 kN-m, M_CD=-52.92 kN-m, M_DC=-51.08 kNm

            Ex.3

Answer for above problem is: M_AB=-28.03 kN-m, M_BA=7.02 kN-m, M_BC=-7.02 kN-m, M_CB=31.64kN-m, M_CD=-31.64 kN-m, M_DC=-27.36 kNm

     Ex.4

Answer for above problem is: M_AB=-16.727 kN-m, M_BA=5.091 kN-m, M_BC=-5.091 kN-m, M_CB=24.364 kN-m, M_CD=-24.364 kN-m, M_DC=0 kNm

        Ex.5

Answer for above problem is: M_AB=91.63 kN-m, M_BA=-65.82 kN-m, M_BC=65.82 kN-m, M_CB=116.35 kN-m, M_CD=-116.35 kN-m, M_DC=81.93 kNm