Installing and Using Openseespy

Slope deflection method for beams

This blog post illustrates the use of the slope-deflection method to analyse indeterminate beams

 The following steps are followed in the slope-deflection method 

1.  Identifying the unknown joint displacements /kinematic indeterminacy/Degree of Freedom (DOFs)
2.  Write slope deflection equations (SDEs) for each member. This includes substituting the fixed end moments (due to span loading) in SDEs, substituting known joint displacements in each SDE
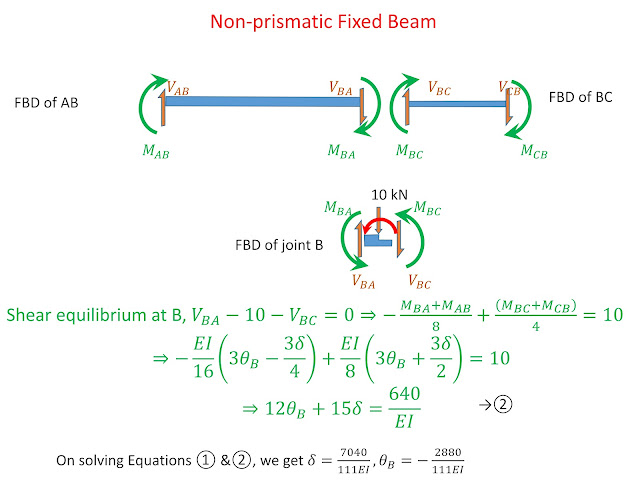
3. Write the joint equilibrium equations for each joint having a DOF. Substituting SDEs in joint equilibrium equations
4. Solve the joint equilibrium equations simultaneously for unknown joint displacements
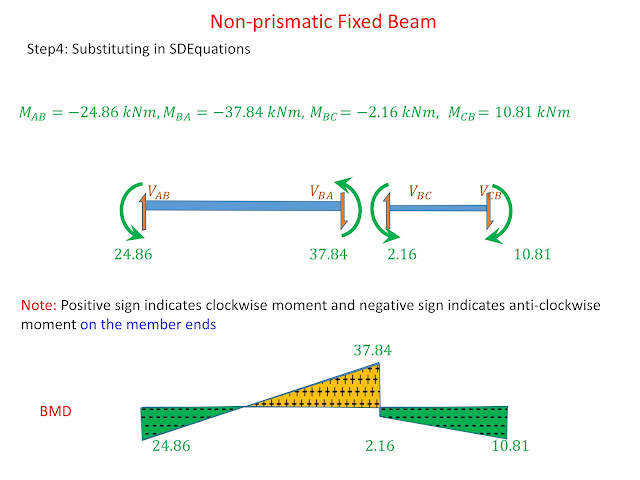
5. Substituting the joint displacements in SDEs to evaluate the member end moments
6. Drawing the deflected shape and BMD for the frame

                 Illustrative Example-1                             

In the two-span continuous beam given below, there is only one kinematic indeterminacy (or unknow joint displacement). That is, the rotation at B (or slope at B)

                             Illustrative Example-2                                          

In this example, there are two unknown joint displacements (Kinematic indeterminacy=2). These are the rotations at joints B and C

            Illustrative Example-3                                

Compatibility Equations

 For the deformed body to have a compatible deformation (deformation without discontinuities), the displacement field formed by the strain components should be continuous. For this to be satisfied, the strains should satisfy the compatibility conditions described as below

Unsymmetrical bending of Beams and shear center