This blog post illustrates the use of the slope-deflection method to analyse indeterminate beams
The following steps are followed in the slope-deflection method
- Identifying the unknown joint displacements /kinematic indeterminacy/Degree of Freedom (DOFs)
- Write slope deflection equations (SDEs) for each member. This includes substituting the fixed end moments (due to span loading) in SDEs, substituting known joint displacements in each SDE
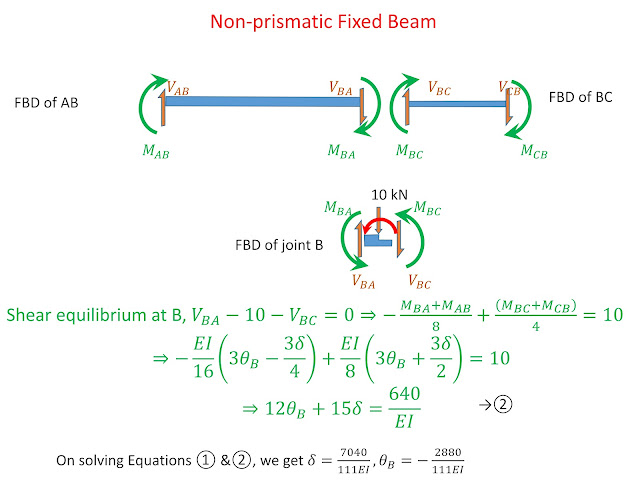
- Write the joint equilibrium equations for each joint having a DOF. Substituting SDEs in joint equilibrium equations
- Solve the joint equilibrium equations simultaneously for unknown joint displacements
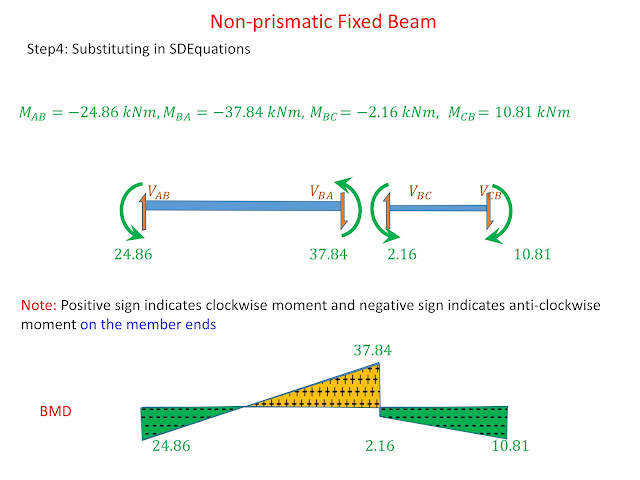
- Substituting the joint displacements in SDEs to evaluate the member end moments
- Drawing the deflected shape and BMD for the frame
Illustrative Example-1
In the two-span continuous beam given below, there is only one kinematic indeterminacy (or unknow joint displacement). That is, the rotation at B (or slope at B)
Illustrative Example-2
In this example, there are two unknown joint displacements (Kinematic indeterminacy=2). These are the rotations at joints B and C
