Stress Invariants and Principal stresses

To determine the roots of a cubic equation using calculator, follow the steps in the video below

Equilibrium equations - Relationship between stress components

 Equilibrium equations - Relationship between stress components

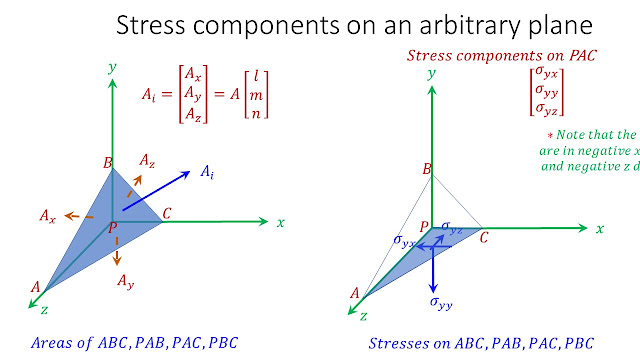
When a body is subjected to loads, stresses are developed in all portions of the body. But, the stresses should develop in such a way that the sum of all forces should be zero, i.e the force balance should be satisfied in all directions, including along x-, y- and z- directions. In the following paragraphs, the relationship between various stress components of a DIFFERENTIAL ELEMENT is derived based on the equilibrium conditions. The resultant relationships are thus referred to as equilibrium equations in 3D.

In addition to the stresses on all the six faces, there can be body forces, which are developed within the volume. For example, the gravity force is developed in proportion to the volume of the differential element considered. Such volume-proportional forces are referred to as body forces. Their contribution is to be considered in the EQUILIBRIUM equations.

Stress Transformations in 3D

 Stress Transformation in 3D

Unit I of Theory of Elasticity

Question Bank for UG students- topic wise links

QUESTION BANK

Topic 1.Static and Kinemetic indeterminacy

 

Topic 2.SFD and BMD of determinate beams 

 These problems are solved by applying equilibrium to suitably cut sections

Topic 3.Beam deflection problems

These problems can be solved by Double integration method, Macaulay's method, Moment area method, Conjugate beam method or strain energy (Castigliano's method or unit Load method)

Topic 4.Determinate Truss Analysis

These problems can be solved by method of joints, method of sections or tension coefficient method

 Topic 5. Truss deflection problems

These problems can be solved by Castigliano's method or unit Load method

Topic 6. Indeterminate beam problems

Answers to the above problems

Rayleigh's method for natural frequencies

 Rayleigh's method for natural frequencies

Rayleigh gave  the following strategy to determine the natural frequencies of dynamic systems.

1. The total response is resolved into spatial and time variations. This is always true for systems vibrating under natural modes
2. Any spatial variation that satisfies the boundary conditions can be assumed. Accordingly, the result will be only approximate.
3. The temporal (time-) distribution will be simple harmonic motion (under natural vibration)
4. Using the total response the expression for the strain energy can be derived
5. Using the total response, the expression for the kinetic energy can also be derived
6. Assuming no damping, the maximum values of strain energy and kinetic energies can be equated to give the expression for natural frequency.

These steps are demonstrated in the figures below

The solution for natural vibration of simply supported beam 

(* This solution assumes that the gravity is absent. Otherwise we will have to consider the change in potential energy during the vibration. Alternatively this can be assumed to be a vertical simply supported column) 

The solution for the above problem can also be derived from first principles as follows

The solution for natural vibration of cantilever beam 

(* This solution assumes that the gravity is absent. Otherwise we will have to consider the change in potential energy due to the vibration. Alternatively this can be assumed to be a vertical cantilever column)

Solution in one step using the derived expression for wn. 

Note that the assumed shape function should satisfy the boundary conditions at the ends

The above solution can also be derived from first principles as follows

Rayleigh method can also be applied to lumped mass system as follows

  From this the Rayleigh coefficient can be calculated as wn2=32/170

From this the Rayleigh coefficient can be calculated as wn2=275/200