Slope Deflection Method for portal Frames

 The following content explains the procedure for 

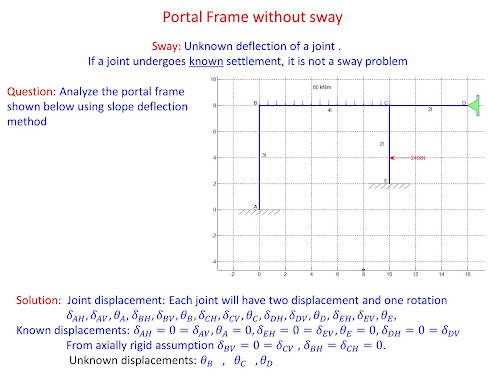
1.  identifying the unknown joint displacements /kinematic indeterminacy/Degree of Freedom (DOFs)
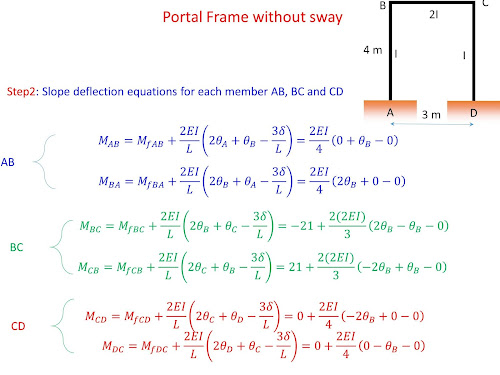
2.  writing slope deflection equations (SDEs) for each member 
3. substituting the fixed end moments (due to span loading) in SDEs
4. substituting known joint displacements in each SDE
5. writing the joint equilibrium equations for each joint having a DOF
6. Substituting SDEs in joint equilibrium equations
7. Solving the joint equilibrium equations simulateously for unknown joint displacements
8. Substituting the joint displacements in SDEs to evaluate the member end moments
9. Drawing the deflected shape and BMD for the frame

Problem 1

Problem 2

Analysis of portal frame "with sway" using Slope deflection method

Exercise Problems:

Ex.1

The UDL on the beam BC is 28 kN/m.

Answer for above problem is: M_AB=5.83 kN-m, M_BA=10.07 kN-m, M_BC=-10.07 kN-m, M_CB=8.9 kN-m, M_CD=-8.9 kN-m, M_DC=-3.04 kNm

       Ex.2

Answer for above problem is: M_AB=-35.08 kN-m, M_BA=-20.92 kN-m, M_BC=20.92 kN-m, M_CB=52.92 kN-m, M_CD=-52.92 kN-m, M_DC=-51.08 kNm

            Ex.3

Answer for above problem is: M_AB=-28.03 kN-m, M_BA=7.02 kN-m, M_BC=-7.02 kN-m, M_CB=31.64kN-m, M_CD=-31.64 kN-m, M_DC=-27.36 kNm

     Ex.4

Answer for above problem is: M_AB=-16.727 kN-m, M_BA=5.091 kN-m, M_BC=-5.091 kN-m, M_CB=24.364 kN-m, M_CD=-24.364 kN-m, M_DC=0 kNm

        Ex.5

Answer for above problem is: M_AB=91.63 kN-m, M_BA=-65.82 kN-m, M_BC=65.82 kN-m, M_CB=116.35 kN-m, M_CD=-116.35 kN-m, M_DC=81.93 kNm