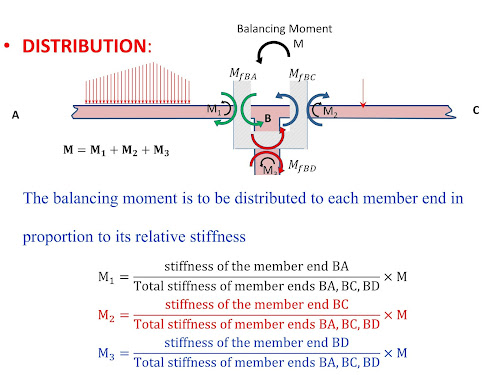
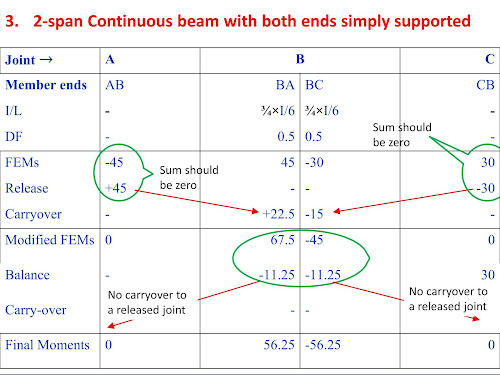
MOment Distribution

 MOMENT DISTRIBUTION METHOD

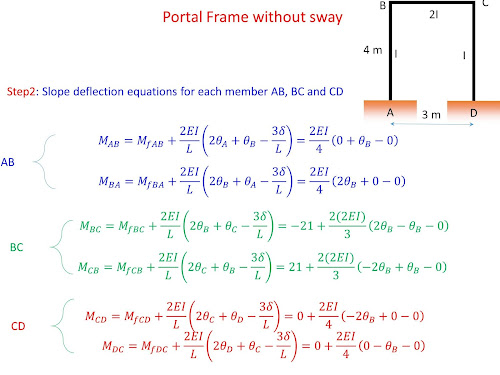
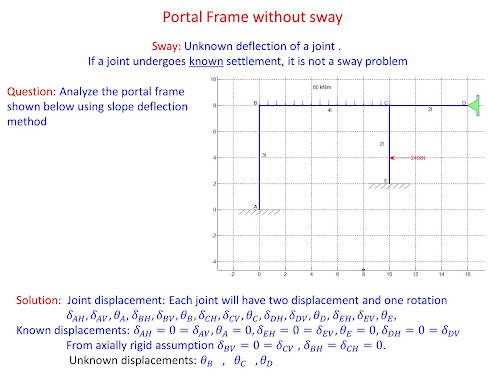
Slope Deflection Method for portal Frames

 The following content explains the procedure for 

1.  identifying the unknown joint displacements /kinematic indeterminacy/Degree of Freedom (DOFs)
2.  writing slope deflection equations (SDEs) for each member 
3. substituting the fixed end moments (due to span loading) in SDEs
4. substituting known joint displacements in each SDE
5. writing the joint equilibrium equations for each joint having a DOF
6. Substituting SDEs in joint equilibrium equations
7. Solving the joint equilibrium equations simulateously for unknown joint displacements
8. Substituting the joint displacements in SDEs to evaluate the member end moments
9. Drawing the deflected shape and BMD for the frame

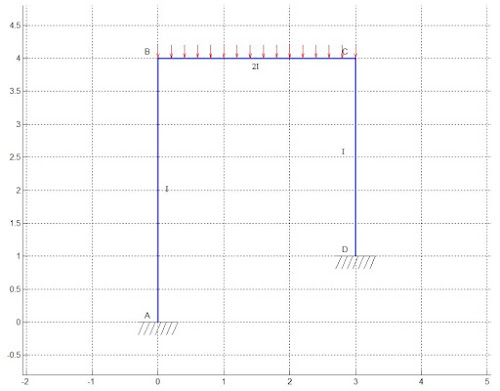
Problem 1

Problem 2

Analysis of portal frame "with sway" using Slope deflection method

Exercise Problems:

Ex.1

The UDL on the beam BC is 28 kN/m.

Answer for above problem is: M_AB=5.83 kN-m, M_BA=10.07 kN-m, M_BC=-10.07 kN-m, M_CB=8.9 kN-m, M_CD=-8.9 kN-m, M_DC=-3.04 kNm

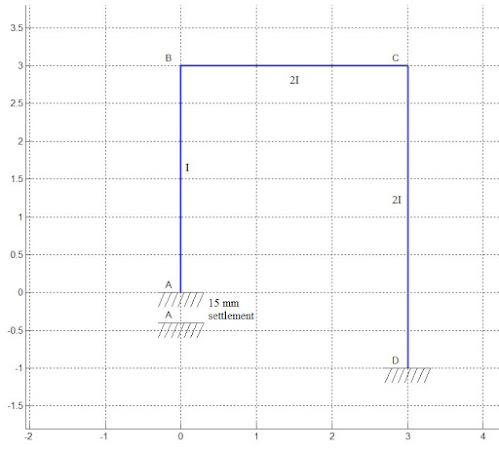
       Ex.2

Answer for above problem is: M_AB=-35.08 kN-m, M_BA=-20.92 kN-m, M_BC=20.92 kN-m, M_CB=52.92 kN-m, M_CD=-52.92 kN-m, M_DC=-51.08 kNm

            Ex.3

Answer for above problem is: M_AB=-28.03 kN-m, M_BA=7.02 kN-m, M_BC=-7.02 kN-m, M_CB=31.64kN-m, M_CD=-31.64 kN-m, M_DC=-27.36 kNm

     Ex.4

Answer for above problem is: M_AB=-16.727 kN-m, M_BA=5.091 kN-m, M_BC=-5.091 kN-m, M_CB=24.364 kN-m, M_CD=-24.364 kN-m, M_DC=0 kNm

        Ex.5

Answer for above problem is: M_AB=91.63 kN-m, M_BA=-65.82 kN-m, M_BC=65.82 kN-m, M_CB=116.35 kN-m, M_CD=-116.35 kN-m, M_DC=81.93 kNm

ABAQUS learnings

 User Subroutines in ABAQUS 

• COMMON BLOCK data: The data stored in COMMON BLOCK can be used by all the subroutines. This data can be imported from external files using UEXTERNALDB user subroutine

       Eg.  common/crdflg/xintm(2,2,10,144),lrdflg,lwrtflg  

      See link here for such problems

• 
  

Design of small industrial building with gantry-II

In this post we will see the design of gable columns and gable wind girder or eave girder

 Gable Column:

Design of small industrial building with gantry-I

Design of  industrial building consists of the design of the following components.

This post deals with the design of the components starting from Gable rafter.

The factors governing the calculation of span length, dead load and wind load are given below

Dead Load : Roof sheeting @0.16 kN/m2, purlins @0.08 kN/m, self wt of gable rafter @ 0.1 kN/m
Live load of 0.5 kN/m2 can be assumed
Wind Load: IS 875-PartIII prescribes the value of C_pe as -0.8 as given below

Design moment: As mentioned in the figures above, the design moment can be taken as if gable rafter is simply supported between the columns. This is conservative and simplified approach.

Design moment capacity: Plastic moment capacity of a selected section can be obtained after locating the palstic neutral axis, as below

Design of Side rails/ Wall girts: 

Side rails suporting the wall sheeting are designed as laterally supported beams subjected to biaxial bending as prescribe in IS 800: 2007

Design loads are calculated based on the design values shown in the above figure. The external wind pressure coefficient is given below in IS 875-part III

Design moments in both directions can be obtained considering the continuous span to be simply supported between the columns

Design plastic moment capacities in both directions can be obtained directly from plastic section moduli given in IS 800-2007

The interaction formulae given below can be used to check this beam under biaxial bending